- Expositor : Dr. Ulises Velasco García
- Institución : Universidad Autónoma de Querétaro, México
- Fecha : Miércoles 11 de noviembre de 2020
- Lugar : Zoom meeting (ID 867 5499 0016, Password 828271)
- Enlace : https://reuna.zoom.us/j/86754990016?pwd=cVA5MTk0ZXFGYmFVQS9SN2RvRklwQT09
- Hora : 18:10 PM -19:00 PM (Santiago Time).
Resumen. La ecuación no lineal de Schrödinger en (1+1) dimensiones es de la forma
![]()
donde la función complejo-valuada q(x, t) es el campo de cambio lento de un pulso de luz propagándose en una fibra óptica
baja la influencia de dispersión cromática y no linealidad material que aparece en el problema físico de la propagación de un solitón, t es la variable de propagación, i es la unidad imaginaria y x es la variable espacial real.
Bajo el contexto de la física teórica la ecuación no lineal de Schrödinger es una generalización en un sentido no lineal de la ecuación de Schrödinger clásica. Se considera una ecuación de campo cuyas principales aplicaciones están relacionadas con la propagación de luz en las fibras ópticas (especialmente de solitones) así como ondas de guía planas, también está relacionada con el modelo que describe el condensado de Bose-Einstein confinado en una trampa altamente anisotrópica en forma de cigarrillo en el régimen del campo promedio. De manera adicional, la ecuación aparece en estudios de ondas gravitacionales de amplitud pequeña en la superficie de agua profunda sin viscosidad. Entre otros ejemplos.
En esta charla nos centramos en el transformada de dispersión directa de la ENLS lo cual se reduce al estudio del
sistema Zakharov-Shabat (Z-S) [1,2,3] de la forma
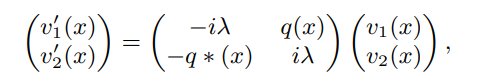
donde v1,2 son funciones complejo valuadas desconocidas, λ es conocido como el parámetro espectral, la función complejo valuada q(x) es el potencial, ∗ es la conjugación en un sentido complejo e i la constante imaginaria. Dado que el sistema Z-S se reduce a las ecuaciones de Sturm-Liouville bajo ciertas restricciones, se muestran, una representación de la solución del sistema de Z-S en términos de series de potencias del parámetro espectral [4] y también se muestra una representación de la solución en términos de la aproximación analítica de los operadores de transmutación [5] para las soluciones del sistema Z-S así como también, a partir de dichas soluciones, se construyen los coeficientes de Fourier no lineales correspondientes.
Al final de la charla se muestran experimentos numéricos, propiedades y características numéricas de cada método, así como un enfoque híbrido aprovechando las mejores cualidades de cada técnica.
Bibliografía
[1] M. J. Ablowitz, H. Segur. Solitons and th Inverse Scattering Transform. 1st ed. Society for industrial and applied mathematics (SIAM), 2000.
[2] M. I. Yousefi, F. R. Kschischang. Information transmission using the nonlinear Fourier transform, part I: Mathematical tools. Submitted to IEEE transactions on information theory. ArXiv:1202.3653v2.
[3] J. K. Shaw. Mathematical principles of optical fiber communications. SIAM, May 1, 2004-93 pages.
[4] V. V. Kravchenko, R. M. Porter. Spectral parameter power series for Sturm-Liouville problems.
Mathematical Methods in the Applied Sciences. Special Issue: Complex-Analytic Methods. Volume 33, Issue 4, pages 459-468, 15 March 2010.
[5] V. V. Kravchenko, S. M. Torba. Analytic approximation of transmutation opperators and applications to highly accurate solution of spectral problems.Journal of Computational and Applied Mathematics, Volume 275, February 2015, Pages 1-26.
[6] Kharif, C.; Pelinovsky, E.; Slunyaev, A. Rogue Waves in the Ocean; Springer: Berlin, Germany, 2009.
[7] Osborne, A. Nonlinear Ocean Waves & the Inverse Scattering Transform; Academic Press: Amsterdam, The Netherlands, 2010; Volume 97.
[8] Babanin, A. Breaking and Dissipation of Ocean Surface Waves; Cambridge University Press: Cambridge, UK, 2011.
- Informaciones: marriag@ubiobio.cl
- Auspiciadores: Dirección de Postgrado-UBB. Departamento de Matemática UBB.
- Trabajo en conjunto con: Prof. Vladislav V. Kravchenko, CINVESTAV-Querétaro., México. Prof. Sergii M. Torba, CINVESTAV-Querétaro, México.
